cucumber flesh

Rを中心としたデータ分析・統計解析らへんの話題をしていくだけ

📈統計的問題を回避するためのデータ解析のプロトコル (Zuur et al. 2010): 8 説明したい変数は独立と言えるのか？

data exploration R time series rWBclimate ggfortify

この記事では統計的問題を回避するためのデータ解析のプロトコル (Zuur et al. 2010)で扱われている目的変数の独立性について議論する。

uribo.hatenablog.com

データ解析時における統計的手法の多くは、観測されたデータが他と独立であることを仮定している。あるデータをとる時、そのデータは以前に観測されたデータとは無関係に集められる必要がある。また新たに得られたデータが今後得られるデータに対して影響を及ぼすような何らかの情報を含んでいてはいけないというようなものである。といってもあくまでもこれらは仮定なので、現実にはこれらが完全に独立でないことを考慮することの方が大事になってくる。

一方で明らかにデータどうしが独立でないものもある。例えば地域を代表する植生を調べた時、調査した地点が互いに近いと同じようなデータが得られてしまい、十分に調査地の距離を離して得たデータと比較した場合には、地域の植生を表現するには不十分だろう。これは調査した地点の距離が近いことによる自己相関である。近い場所では同じような植生があるだろうし、遠くへ行けば異なる景観となるだろう（あるいはその逆）というのは直感的に予測できるものである。このようにデータの性質によって自己相関を生じやすいデータがある。特に空間や時間は自己相関を示す典型的なデータである。

次にあげるいくつかの項目について比較した場合、前者と後者、どちらの方が似た結果を得るだろうか。またデータの結果が異なってくるのはどちらであろうか。

  • 一週間毎日、定期的に記録した日平均気温(a)と、過去30年間の年平均気温(b)
  • 駅の周辺にいる人を対象にしたアンケート(a)と世界各地の駅周辺で集めたアンケート(b)
  • 特定の分類群を対象にした生物の調査(a)とさまざまな分類群が含まれたデータ(b)

こうしたデータは互いに他のデータに影響を及ぼす代表的なものである。もしこのような性質をもつデータを通常のデータと同様の統計解析を行った場合、特に自己相関をもつ変数の予測を行うようなモデリングや２変数の単回帰を行った時には意図しない結果や問題を生じることがある。とりわけ統計モデリングにおける第１種の過誤を犯す確率が高くなることが指摘されることが多い (Legendre and Desdevises 2009; Baayen et al. 2016)。

例えば昨年に出たR本「新米探偵、データ分析に挑む（石田 2015）」でも時系列のデータが扱われており、ちょっとした議論があった。

新米探偵、データ分析に挑む

新米探偵、データ分析に挑む

d.hatena.ne.jp

blog.goo.ne.jp

このような時間によって変化するある変数について統計モデリングを行う際の問題については北海道大学の久保さんの資料にもある (PDF)が、Rに備わっているデータを使って考えてみたい。

Rでは標準のデータセットとして時系列データが豊富に備わっており、treeringというデータを使ってみる。このデータセットはDonald A. Graybillによって1980年に調べられたカリフォルニア州のマツ科樹木の年輪幅（樹木の成長指標となる）のデータである。推定された年輪幅についてB.C.6000年からA.D.1979年までの値がある。

data("treering")
str(treering)

##  Time-Series [1:7980] from -6000 to 1979: 1.34 1.08 1.54 1.32 1.41 ...

この年輪データについて、統計モデリングをするために樹木の成長に影響を及ぼすであろう要因として、年の変数に加えて「年平均気温」を与えてみたい。{rWBclimate}パッケージを使えば、簡単に世界の気候データが利用できるのでそれを用いる（The Climate Data API http://data.worldbank.org/developers/climate-data-api を利用している）。なお、取得できる気温の値が1901年からのものなので、以降は年輪データも1901年からのものを対象にする。

# 年輪データのデータフレームを作成する
df_treering <- treering %>% unclass() %>% 
    dplyr::data_frame(width = ., year = time(.)) %>% 
    dplyr::filter(year >= 1901 & year < 1979)
# 気候データの取得
library(rWBclimate)
df_grob_temp <- get_historical_temp(locator = "USA", 
    time_scale = "year") %>% dplyr::select(-locator) %>% 
    dplyr::rename(temp = data)
# 二つのデータフレームを結合する
df_treering %<>% dplyr::inner_join(., df_grob_temp)
# データフレームの中身を確認
dplyr::glimpse(df_treering)

## Observations: 78
## Variables: 3
## $ width (dbl) 1.274, 1.006, 1.083, 0.882, 1.409, 1.113, 1.274, 1.356, ...
## $ year  (dbl) 1901, 1902, 1903, 1904, 1905, 1906, 1907, 1908, 1909, 19...
## $ temp  (dbl) 6.618749, 6.464327, 6.073844, 6.149883, 6.599617, 6.5228...

年輪幅の変化を推定するための一般化線形モデル（年輪幅 width ~ 年 year + 年平均気温 temp）を適用してみる。

df_treering %>% glm(width ~ year + temp, 
    data = ., family = Gamma(link = "log")) %>% 
    broom::tidy() %>% knitr::kable(format = "markdown")
term estimate std.error statistic p.value
(Intercept) 5.6334687 2.6433161 2.1312126 0.0363483
year -0.0029395 0.0013811 -2.1283725 0.0365908
temp 0.0100788 0.0797796 0.1263335 0.8998060

というように、年輪幅に影響する変数として年が気温よりも有意に効いている（P < 0.05）という結果が得られた。実際に両者の値をプロットしてみると、あたかも関係がありそうな感じもある。

df_treering %>% ggplot(aes(year, width)) + 
    geom_point() + geom_line(alpha = 0.4) + 
    stat_smooth(method = "lm", se = FALSE, 
        colour = "tomato")

f:id:u_ribo:20160202130051p:plain

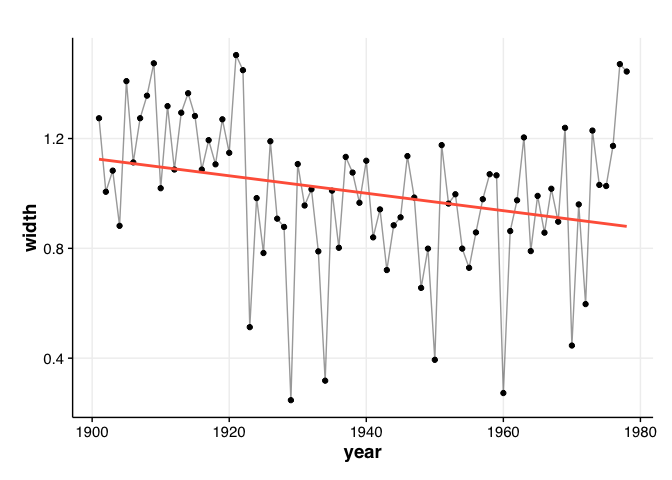
しかし、このような時系列データでこのような統計モデリングを行うのは間違いである。年ごとに変化する年輪幅のようなデータでは、ある年の値は前年の値に影響を受けているし、また同様にある年の値は次の年の値に直接影響する。

考えてみればこれらは当然のように思えるかもしれないが、ではデータがどれだけ他と離れていれば独立であると言えるのだろう。独立性を確かめる方法は必ずしも簡単というわけではない。

自己相関を検出するための第一歩

それではこのような自己相関をもたらす変数を扱う場合にはどのように対処すれば良いかというとそれはデータの種類に応じてさまざま...ということになるが、まずはデータが自己相関しているのかを確かめることから始めてみたい。変数の自己相関を確認するための手法として、Rではコレログラムと呼ばれる横軸に時間のラグ（時間_{t + lag}）、縦軸に自己相関係数をプロットした図を描画する関数が用意されている。

時系列データの可視化には、標準のplot()関数でも良いが、{ggplot2}をインポートしている {ggfortify}パッケージの利用するのが良い（好みの問題）。

library(ggplot2)
library(ggfortify)
# 上の図もこのオレオレテーマを使用した
theme_set(SUmisc:::theme_Publication())

acf()関数は自己相関と自己共分散の視覚化のために利用できる。青い破線は自己相関係数が０であることを帰無仮説とした場合の95%信頼区間である。

# この場合の1ラグは1年間
acf(AirPassengers, type = "correlation", 
    plot = FALSE, lag.max = 50) %>% autoplot(colour = "tomato")

f:id:u_ribo:20160202130210p:plain

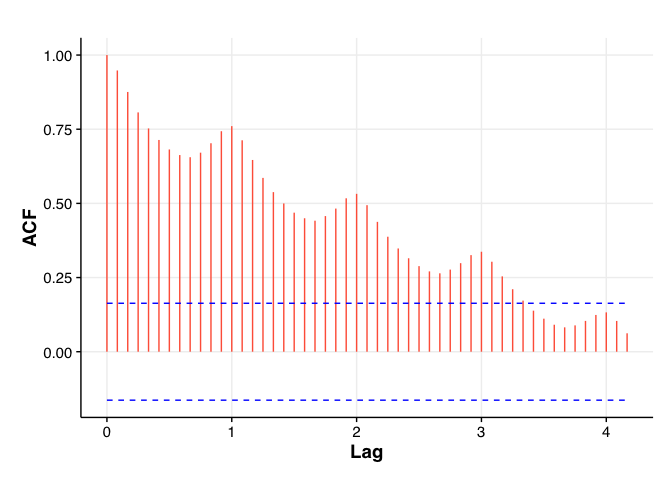
この図ではラグ3.5まで有意な自己相関を検出している。またラグ１の状態では自己相関係数0.760と強い正の相関を示していることがわかる。

自己相関を解決するために

自己相関が生じる要因によって用いるべき分析手法が異なる。自分の知っている範囲でこれらの手法を扱っている以下の書籍・文献が参考になると思われるのであげておく。

空間的自己相関... Moran's I, Non-metric multidimensional scalingなど

時間的自己相関... 自己回帰モデル、一般化加法混合モデルなど

  • Baayen, R. H., van Rij, J., de Cat, C., & Wood, S. N. (2016). Autocorrelated errors in experimental data in the language sciences: Some solutions offered by Generalized Additive Mixed Models... 先月出N. S. Woodらの文献。実例を交えて彼らの開発している{mgcv}パッケージを使った時系列データ分析の注意点について触れている。
  • Analysing Ecological Data (Statistics for Biology and Health)

系統的自己相関... 系統的独立対比、Phylogenetic generalized least squares linear regressionなど

参考

  • 石田基広 (2015). 新米探偵、データ分析に挑む. ソフトバンククリエイティブ
  • Baayen, R. H., van Rij, J., de Cat, C., & Wood, S. N. (2016). Autocorrelated errors in experimental data in the language sciences: Some solutions offered by Generalized Additive Mixed Models
  • Legendre, P., & Desdevises, Y. (2009). Independent contrasts and regression through the origin. doi:10.1016/j.jtbi.2009.04.022

実行環境

devtools::session_info() %>% {
    print(.$platform)
    .$packages %>% dplyr::filter(`*` == "*") %>% 
        knitr::kable(format = "markdown")
}

##  setting  value                       
##  version  R version 3.2.3 (2015-12-10)
##  system   x86_64, darwin13.4.0        
##  ui       X11                         
##  language En                          
##  collate  en_US.UTF-8                 
##  tz       Asia/Tokyo                  
##  date     2016-02-02
package * version date source
ggfortify * 0.1.0 2015-11-30 CRAN (R 3.2.2)
ggplot2 * 2.0.0 2015-12-18 CRAN (R 3.2.3)
magrittr * 1.5 2016-01-13 Github ()
proto * 0.3-10 2012-12-22 CRAN (R 3.1.0)
rWBclimate * 0.1.3 2014-04-19 CRAN (R 3.2.0)